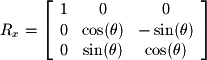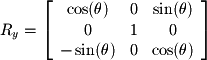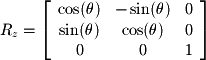Several common linear transformations show up in linear algebra and in other fields which are based on linear algebra. The ones we will discuss here are orthogonal projections, reflections, and rotations. For simplicity and visualization, we will remain in 
and 
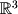but these transformations can be applied in any N-dimensional space. Orthogonal projections are the simplest. Consider the shadow cast on a sidewalk by an overhang on a sunny day. We would say that the shadow is a projection of the overhang onto the sidewalk. Now if the sun is directly over the overhang (at a 
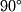angle), the shadow cast is an orthogonal projection. Thus if we have a vector in 
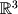we can find its orthogonal projection onto the xy-plane by dropping the z coordinate. Formally, this can be written in matrix form as the following:
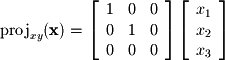Notice that this transformation preserves 
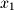and 
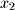but drops the last coordinate 
.
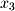Instead of projecting onto the xy-plane, let's say we want to reflect across it. This transformation consists of negating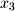
and can be written as the following:
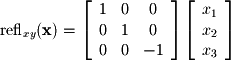Finally, we move to the most common and useful transformation: rotations. To place rotations in context, consider that every software application which uses 3D graphics has at its core rotation matrices. These matrices orient objects within a scene relative to one another and orient the entire scene with respect to the user. In a complex engineering design package or 3D game, several hundred of these transformations may need to be computed every second in order to render the 3D scene. It is especially useful to note that the matrix representation is a very efficient way to store and compute these transformations. So, with that preface, let's start with the 2D rotation matrix. In order to derive this matrix we will define a rotating coordinate system 
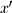and 
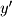as shown in Figure x.
Needs to draw another rotated axis of a different color
Given the x and y coordinates of a single point, we need a way to find its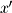
and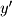 
coordinates. These are easy to find using basic trigonometry:
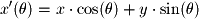Since we know 
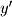will always be 
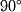from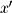 
we can easily find 
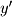as the following:
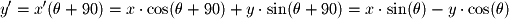We can now write these two equations in matrix form to give the linear transformation for 2D rotations:
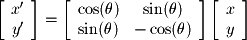We will not derive the matrices for 3D transformations here, but they can be derived in a similar fashion as that shown above. The following matrices define rotations around the x, y, and z axes in 
:
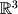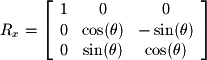
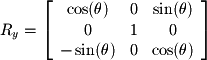
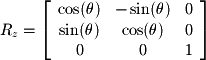
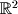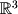and but these transformations can be applied in any N-dimensional space. Orthogonal projections are the simplest. Consider the shadow cast on a sidewalk by an overhang on a sunny day. We would say that the shadow is a projection of the overhang onto the sidewalk. Now if the sun is directly over the overhang (at a 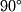angle), the shadow cast is an orthogonal projection. Thus if we have a vector in 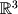we can find its orthogonal projection onto the xy-plane by dropping the z coordinate. Formally, this can be written in matrix form as the following: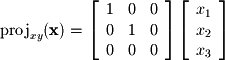 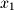and 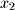but drops the last coordinate 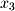.Instead of projecting onto the xy-plane, let's say we want to reflect across it. This transformation consists of negating
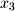and can be written as the following: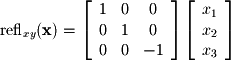 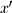and 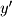as shown in Figure x.Needs to draw another rotated axis of a different color
Given the x and y coordinates of a single point, we need a way to find its
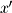and 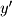coordinates. These are easy to find using basic trigonometry: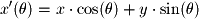 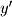will always be 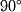from 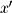we can easily find 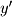as the following: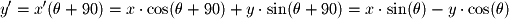:
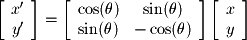