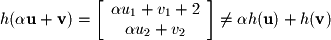A transformation maps an input from one set (domain) to an output of the same or another set (range). In other words, in the context of linear algebra, the terms transformation and function are synonymous. A linear transformation is a transformation for which the following holds: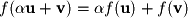 
The term linear implies two properties: additivity and homogeneity. Two functions are additive 
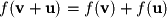and homogeneous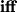 
.
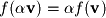A test of linearity can always be applied by using the above properties, but it is normally not required (unless specifically asked for) since linearity is usually a fairly obvious feature when one knows what to look for. For example, the following are all nonlinear functions (transformations):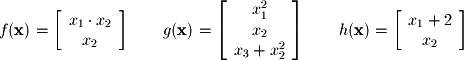
The first row of 
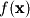is nonlinear, the first and last rows of 
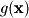are nonlinear, and the first row is nonlinear in 
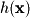. Some things to look for which will lead to nonlinearity are any multiplication of variables, addition of constants, or nonlinear functions on variables (such as squared or cubed).
If you need to formally show linearity, then apply the definition of a linear transformation above. Consider for this example the linear function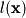
: 
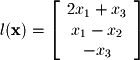By applying the definition of a linear transform we have: 
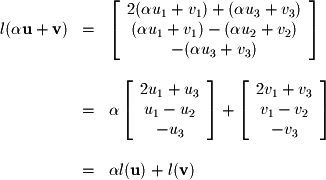If the function had been nonlinear, as in the case of 
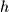, you would not have been able to expand it by applying rules of additivity and homogeneity: 
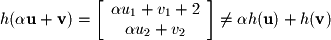The last notable property of linear transformations is that every linear transformation can be written as a system of linear equations and vice versa. That means that many of the techniques that we will learn for dealing with one can be easily applied to the other.
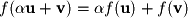
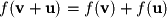and homogeneous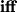 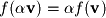.A test of linearity can always be applied by using the above properties, but it is normally not required (unless specifically asked for) since linearity is usually a fairly obvious feature when one knows what to look for. For example, the following are all nonlinear functions (transformations):
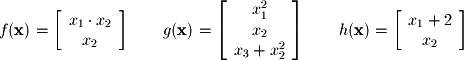
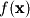is nonlinear, the first and last rows of 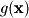are nonlinear, and the first row is nonlinear in 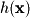. Some things to look for which will lead to nonlinearity are any multiplication of variables, addition of constants, or nonlinear functions on variables (such as squared or cubed).If you need to formally show linearity, then apply the definition of a linear transformation above. Consider for this example the linear function
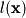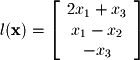
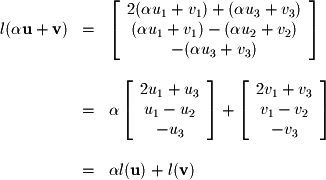
: , you would not have been able to expand it by applying rules of additivity and homogeneity: