Given an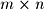 
matrix 
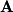, the four fundamental subspaces of Linear Algebra for 
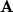are described in the table below:
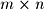matrix 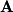, the four fundamental subspaces of Linear Algebra for 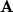are described in the table below: Name | Function | Space | Dimension |
Column Space or Image |  |  |  |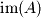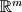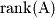
Row Space or Coimage |  |  |  |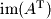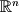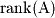
Nullspace or Kernel |  |  |  |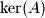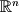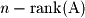
Left Nullspace or Cokernel |  |  |  |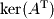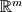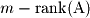
The terms column space and image as well as null space and kernel are used interchangably depending on the text you are using. Until you get used to the terms, this text uses both. The functions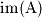 
and 
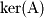are commonly used functional forms to denote the column space (image) and null space (kernel). In this subsection we will discuss how to find basis sets for these spaces given a matrix. We already know how to find a basis for column space (image). Simply row reduce the matrix and take the pivotal columns as the basis. For row space (coimage), first transpose the matrix and then take the pivotal columns of the transposed matrix as the basis.
Finding the null space (kernel) also employs a process we have learned previously. The null space (kernel) is simply the solution space of the system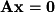
. So the parameterization of the solution gives the vectors that make up the basis.
Finally, there are two ways to find the left null space (cokernel). The left null space is made up of the last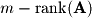
rows of 
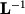where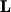 
is the lower-triangular matrix from the 
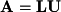factorization. However, an easier way to find the left null space is to transpose the matrix A and row reduce to fi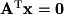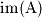nd 
.
and 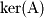are commonly used functional forms to denote the column space (image) and null space (kernel). In this subsection we will discuss how to find basis sets for these spaces given a matrix. We already know how to find a basis for column space (image). Simply row reduce the matrix and take the pivotal columns as the basis. For row space (coimage), first transpose the matrix and then take the pivotal columns of the transposed matrix as the basis.Finding the null space (kernel) also employs a process we have learned previously. The null space (kernel) is simply the solution space of the system
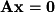. So the parameterization of the solution gives the vectors that make up the basis.Finally, there are two ways to find the left null space (cokernel). The left null space is made up of the last
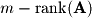rows of 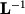where 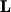is the lower-triangular matrix from the 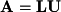factorization. However, an easier way to find the left null space is to transpose the matrix A and row reduce to find .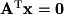