The term linear combination is fundamental to linear algebra and will be used throughout this text. A linear combination of a set of vectors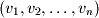 
can be defined as the addition of these vectors scaled by a corresponding ordered set of scalar coefficients 
:
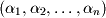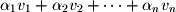For example, let's consider the following 3 vectors:
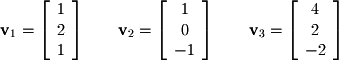In this case, 
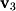is a linear combination of 
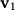and 
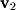. Close inspection shows that 
:
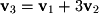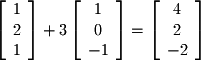This linear combination is illustrated graphically in Figure 2-4 where you can see that 
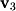is composed of 1 
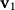and 3 
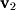's.
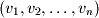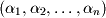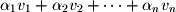
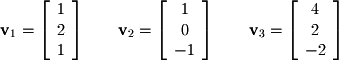
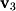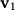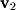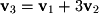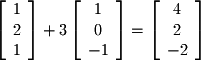
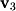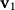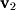can be defined as the addition of these vectors scaled by a corresponding ordered set of scalar coefficients : is a linear combination of and . Close inspection shows that : is composed of 1 and 3 's. Object could not be loaded.
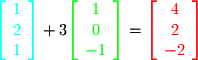
Figure 2-4.
Geometry of a Linear Combination
Linear combinations will often be used to define more complex mathematical sets or geometric objects. For example, a line in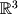 
is defined as the combination of a starting vector (in this case 
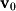) with a direction vector (
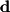) which is scaled by a "free parameter" 
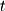. The term free parameter simply states that the scalar value is free to take on any real value between positive and negative infinity or in interval notation 
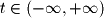. Figure 2-5 illustrates how this linear combination maps out a line in 
.
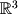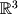is defined as the combination of a starting vector (in this case 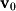) with a direction vector (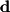) which is scaled by a "free parameter" 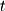. The term free parameter simply states that the scalar value is free to take on any real value between positive and negative infinity or in interval notation 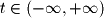. Figure 2-5 illustrates how this linear combination maps out a line in 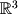. Object could not be loaded.
Figure 2-5.
Parameterized Line (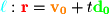
)
)
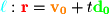