In order to deal with higher dimensional spaces, we generalize concepts such as numbers and sets to higher dimensions. We will start by defining 1-dimensional finite sets which you may have encountered in elementary algebra. A set is any unordered collection of distinct objects of any type. The following are examples of finite sets: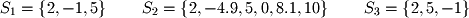
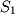is called an integer set because it contains only whole numbers while 
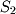is a real set because it contains decimals. Order does not matter in sets so the sets 
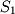and 
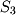are equivalent. Elements of a set are called members. The element symbol 
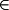defines a variable as belonging to a particular set. 
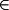is commonly pronounced "in" while reading. For example, 
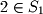should be read "2 in 
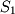". The "not in" symbol 
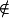says that a member does not belong to a set. For example, 
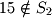states that the member 15 does not belong to 
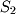. These examples illustrate the use of formal mathematical notation that will be used throughout this book. When a new notation is introduced, care will be taken to explain what it means in simple English. Many students in introductory coursework skip over mathematical notation that they do not understand in textbooks and thus miss important aspects of math theory. You should take the time to become familiar with formal notation when it is introduced because it will help significantly with your understanding of more complex concepts.
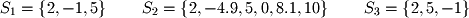
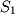is called an integer set because it contains only whole numbers while 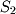is a real set because it contains decimals. Order does not matter in sets so the sets 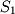and 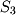are equivalent. Elements of a set are called members. The element symbol 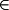defines a variable as belonging to a particular set. 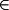is commonly pronounced "in" while reading. For example, 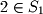should be read "2 in 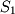". The "not in" symbol 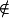says that a member does not belong to a set. For example, 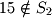states that the member 15 does not belong to 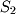. These examples illustrate the use of formal mathematical notation that will be used throughout this book. When a new notation is introduced, care will be taken to explain what it means in simple English. Many students in introductory coursework skip over mathematical notation that they do not understand in textbooks and thus miss important aspects of math theory. You should take the time to become familiar with formal notation when it is introduced because it will help significantly with your understanding of more complex concepts.