In addition to finite sets, we also commonly deal with infinite sets. The standard number lines as shown in Figures 1-5 and 1-6 are examples of a 1-dimensional infinite set. Note that only some of the values in this set are labeled.
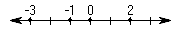 Figure 1-5. 1D Integer Set  | 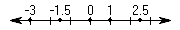 Figure 1-6. 1D Real Set  |
Any infinite set of integers is denoted with a special type of outlined capital letter 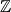 . Any infinite set of reals is written with the symbol
. Any infinite set of reals is written with the symbol 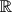 . The integer and real number lines are 1-dimensional sets and thus are written as
. The integer and real number lines are 1-dimensional sets and thus are written as 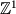 and
and 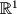 respectively. Using the element symbol we can write statements such as
respectively. Using the element symbol we can write statements such as 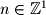 which means that the variable
which means that the variable  can only represent integer numbers. Also, members of such sets are represented geometrically as points. Points are considered
can only represent integer numbers. Also, members of such sets are represented geometrically as points. Points are considered 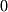 -dimensional objects.
-dimensional objects.
In linear algebra we will deal with sets of greater than 1-dimension. A real set of N-dimensions is written as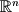 . The 2 dimensional Cartesian coordinate plane is an example of a 2-dimensional infinite real set (
. The 2 dimensional Cartesian coordinate plane is an example of a 2-dimensional infinite real set (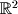 ) as shown in Figure 1-7. Note that since this is a 2-dimensional set, its members have to be specified with 2 numbers.
) as shown in Figure 1-7. Note that since this is a 2-dimensional set, its members have to be specified with 2 numbers.
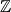 . Any infinite set of reals is written with the symbol
. Any infinite set of reals is written with the symbol 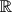 . The integer and real number lines are 1-dimensional sets and thus are written as
. The integer and real number lines are 1-dimensional sets and thus are written as 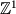 and
and 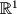 respectively. Using the element symbol we can write statements such as
respectively. Using the element symbol we can write statements such as 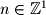 which means that the variable
which means that the variable  can only represent integer numbers. Also, members of such sets are represented geometrically as points. Points are considered
can only represent integer numbers. Also, members of such sets are represented geometrically as points. Points are considered 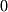 -dimensional objects.
-dimensional objects.In linear algebra we will deal with sets of greater than 1-dimension. A real set of N-dimensions is written as
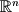 . The 2 dimensional Cartesian coordinate plane is an example of a 2-dimensional infinite real set (
. The 2 dimensional Cartesian coordinate plane is an example of a 2-dimensional infinite real set (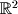 ) as shown in Figure 1-7. Note that since this is a 2-dimensional set, its members have to be specified with 2 numbers.
) as shown in Figure 1-7. Note that since this is a 2-dimensional set, its members have to be specified with 2 numbers. 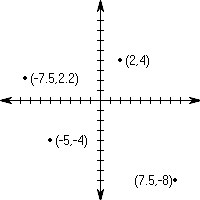
Figure 1-7.
2D Real Set 
A subset is a set within a set. For example, a line is a 1-D subset of  . The following table shows the geometric representation of a set based on its dimensions.
. The following table shows the geometric representation of a set based on its dimensions.
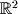 . The following table shows the geometric representation of a set based on its dimensions.
. The following table shows the geometric representation of a set based on its dimensions. Object | Dimension |
Point | 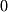 dimensions dimensions |
Line | 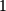 dimension dimension |
Plane | 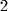 dimensions dimensions |
Hyperplane | 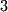 or greater dimensions or greater dimensions |