A vector is a quantity that has magnitude and direction. For example, a velocity of 70 MPH North is a vector quantity because it has a magnitude of 70MPH and a direction of North. The most common vector notations are a bold-faced lower case letter  and a letter with an overhead arrow
and a letter with an overhead arrow 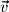 . In contrast to a vector, a quantity with only magnitude is called a scalar. A vector is distinctly different than a point; however, students often confuse the two since both can be written as a grouping of numbers. The following shows the definition of a 3D vector
. In contrast to a vector, a quantity with only magnitude is called a scalar. A vector is distinctly different than a point; however, students often confuse the two since both can be written as a grouping of numbers. The following shows the definition of a 3D vector  and a 3D point
and a 3D point 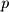 :
: 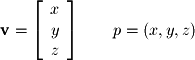 The main distinction between a vector and a point is that two points are equivalent only if they share exactly the same coordinates
The main distinction between a vector and a point is that two points are equivalent only if they share exactly the same coordinates  ,
, 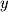 , and
, and  . Two vectors are equivalent if they have the same magnitude and direction. A vector can be visualized graphically as a directed line segment with a starting point and an end point. If the starting point for a vector is not specified it is generally assumed that the starting point is the origin (
. Two vectors are equivalent if they have the same magnitude and direction. A vector can be visualized graphically as a directed line segment with a starting point and an end point. If the starting point for a vector is not specified it is generally assumed that the starting point is the origin (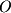 ). In Figure 1-8, the vector
). In Figure 1-8, the vector 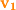 has its tail at the origin (
has its tail at the origin (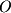 ) and its head at the end point
) and its head at the end point 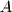 . Although vector
. Although vector 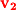 starts at point
starts at point 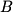 and ends at
and ends at 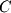 , it is equivalent to vector
, it is equivalent to vector 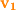 since they both have the same magnitude and direction.
since they both have the same magnitude and direction.
 and a letter with an overhead arrow
and a letter with an overhead arrow 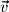 . In contrast to a vector, a quantity with only magnitude is called a scalar. A vector is distinctly different than a point; however, students often confuse the two since both can be written as a grouping of numbers. The following shows the definition of a 3D vector
. In contrast to a vector, a quantity with only magnitude is called a scalar. A vector is distinctly different than a point; however, students often confuse the two since both can be written as a grouping of numbers. The following shows the definition of a 3D vector  and a 3D point
and a 3D point 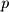 :
: 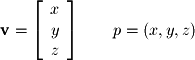
 ,
, 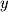 , and
, and  . Two vectors are equivalent if they have the same magnitude and direction. A vector can be visualized graphically as a directed line segment with a starting point and an end point. If the starting point for a vector is not specified it is generally assumed that the starting point is the origin (
. Two vectors are equivalent if they have the same magnitude and direction. A vector can be visualized graphically as a directed line segment with a starting point and an end point. If the starting point for a vector is not specified it is generally assumed that the starting point is the origin (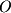 ). In Figure 1-8, the vector
). In Figure 1-8, the vector 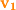 has its tail at the origin (
has its tail at the origin (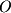 ) and its head at the end point
) and its head at the end point 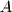 . Although vector
. Although vector 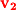 starts at point
starts at point 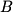 and ends at
and ends at 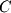 , it is equivalent to vector
, it is equivalent to vector 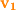 since they both have the same magnitude and direction.
since they both have the same magnitude and direction. Object could not be loaded.
Figure 1-8.
Vectors 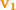 and
and 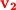
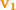 and
and 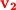
Since we will often refer to a vector with arbitrary 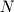 dimensions (rather than with a specific number of dimensions like in the 3 dimensional vector above), it is useful now to point out the formal notation for a vector of length
dimensions (rather than with a specific number of dimensions like in the 3 dimensional vector above), it is useful now to point out the formal notation for a vector of length 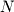 :
: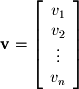 The "dots" are ellipses and represent all the values that are assumed to exist between
The "dots" are ellipses and represent all the values that are assumed to exist between 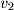 and
and 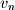 . It is common in mathematics to write a finite series as
. It is common in mathematics to write a finite series as 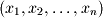 because the first value
because the first value 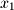 specifies the initial subscript. The second value specifies the direction of the series which in this example is increasing. For example if the second subscript had been
specifies the initial subscript. The second value specifies the direction of the series which in this example is increasing. For example if the second subscript had been 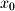 as in the case of
as in the case of 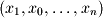 the sequence would have been decreasing. The final
the sequence would have been decreasing. The final 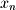 specifies that the sequence terminates at the
specifies that the sequence terminates at the 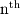 value and thus is a finite sequence.
value and thus is a finite sequence.
Finally, the other vector you will encounter throughout this text is the zero vector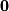 :
: 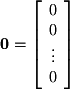 The zero vector is written as a bold-faced
The zero vector is written as a bold-faced 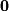 or a zero with an arrow
or a zero with an arrow 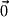 . You should be aware when you see it that the zero vector is not the same as a single scalar
. You should be aware when you see it that the zero vector is not the same as a single scalar 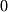 .
.
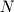 dimensions (rather than with a specific number of dimensions like in the 3 dimensional vector above), it is useful now to point out the formal notation for a vector of length
dimensions (rather than with a specific number of dimensions like in the 3 dimensional vector above), it is useful now to point out the formal notation for a vector of length 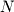 :
: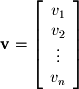
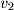 and
and 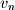 . It is common in mathematics to write a finite series as
. It is common in mathematics to write a finite series as 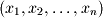 because the first value
because the first value 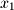 specifies the initial subscript. The second value specifies the direction of the series which in this example is increasing. For example if the second subscript had been
specifies the initial subscript. The second value specifies the direction of the series which in this example is increasing. For example if the second subscript had been 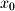 as in the case of
as in the case of 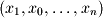 the sequence would have been decreasing. The final
the sequence would have been decreasing. The final 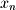 specifies that the sequence terminates at the
specifies that the sequence terminates at the 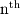 value and thus is a finite sequence.
value and thus is a finite sequence.Finally, the other vector you will encounter throughout this text is the zero vector
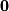 :
: 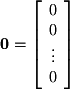
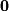 or a zero with an arrow
or a zero with an arrow 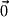 . You should be aware when you see it that the zero vector is not the same as a single scalar
. You should be aware when you see it that the zero vector is not the same as a single scalar 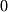 .
.